Activity: The Master Theorem
Learning Goals
You will work towards being able to…
-
State the definition of the Master Theorem
-
Determine the runtime complexity of recursive functions
-
Use the Master Theorem to understand when a divide and conquer approach results in a faster algorithm
Instructions
For each of the following growth functions, solve the recurrence informally, unrolling the recurrence or drawing the recurrence tree (described below) and determine which terms will dominate the time complexity. Then compare your intuitions to the result you get by applying the Master Theorem.
To draw a recurrence tree, you represent each call with a node, where the node is labeled with the time complexity done for that call at that recursive depth and has children that correspond to each recursive call made when executing that function call. This is useful because then we can think of the total work done by the algorithm as the sum of all of the work done at each node. Observe that since leaves have no children, they represent calls that enter the base case! For example, for MergeSort, our structure would look something like the below image, which should look like what you saw in lecture.
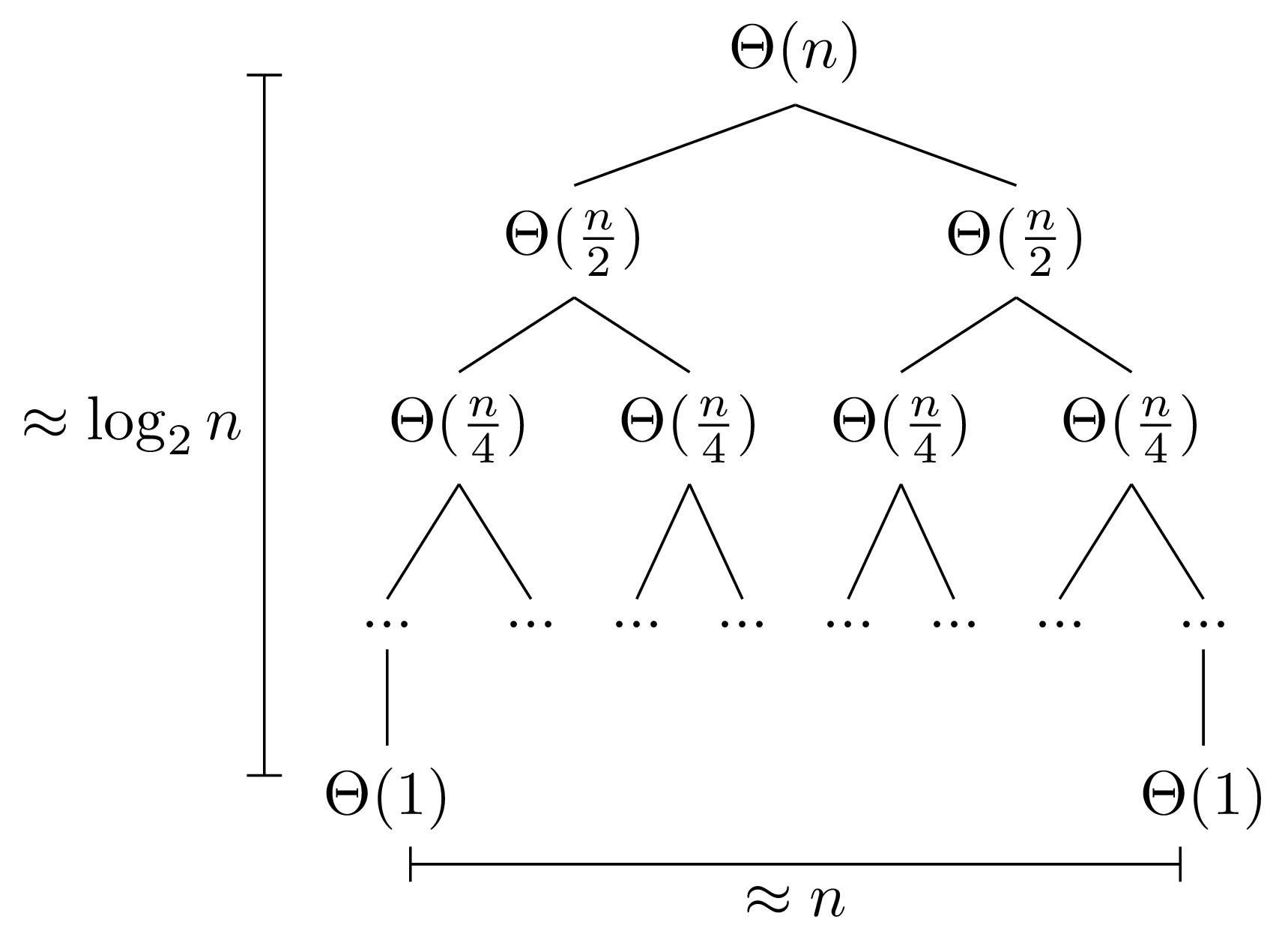
Each function represents the time complexity of a call to Merge, which dominates the non-recursive portion of each call to MergeSort, and that node’s children represent the recursive calls made from that initial call. Note that we work out the height of our tree (how many recursions until our problem size is 1?) and the number of leaves in our tree (after all of our recursions, how many branches do we create?). Then observe that the sum of all of these runtimes is our total runtime!
As you draw and analyze each tree, pay attention to which terms will dominate the total runtime. Then compare your findings to the master theorem
-
$T(n) = 2T(\frac{n}{3}) + n^2$
-
$T(n) = 3T(\frac{n}{2}) + n$
-
$T(n) = 4T(\frac{n}{2}) + n^2$
Submission
Submit an artifact of your work from either 1 or 2 or 3.