Activity 13: Graph Traversal

Learning Goals

You will work towards being able to…

1. Familiarize yourself with common algorithms (Depth \& Breadth First Search)

2. Translate problem specifications into graph problems to be solved with standard algorithms.

Warm-Up: Two-Tabled Wedding (Skiena 7-15):

You are organizing seating for a wedding where all guests in a list $V$ must be organized into two tables. You also have a list $E$ of pairs of people who hate each other. Discuss how you might, if possible, construct a table assignment that avoids any enemies being at the same table. What kind of a graph problem is this?

Instructions

Work with your groups on the following problems. You may work on them in any order:

Articulate a Plan

Let’s dig a bit further into finding articulation points (sometimes called cut-vertices) in a graph. Draw a DFS tree starting at A, and annotate that tree with (1) the depth of each node within the tree, (2) dashed lines for the backward edges, and finally (3) the smallest depth of the node or non-parent neighbors of that node (i.e. backward edges or the depth of the node itself). Call this 3rd value the 1-step high-point of the vertex. ¹

What do you notice about the 1-step high-points of children of articulation vertices (identify the articulation vertices visually at first, then look at the 1-step high-points of their children)? Their descendents? See if you can generalize: Is there a new value at each vertex you should actually keep track of?

Compare these to the conditions of of being an articulation vertex outlined in Skiena (how does the measure you want to construct relate to Skiena’s reachable vertices?).

Then write out pseudocode for this specific articulation vertex finding algorithm (not the genericized version Skiena gives you to demonstrate that it’s a variant of BFS!)

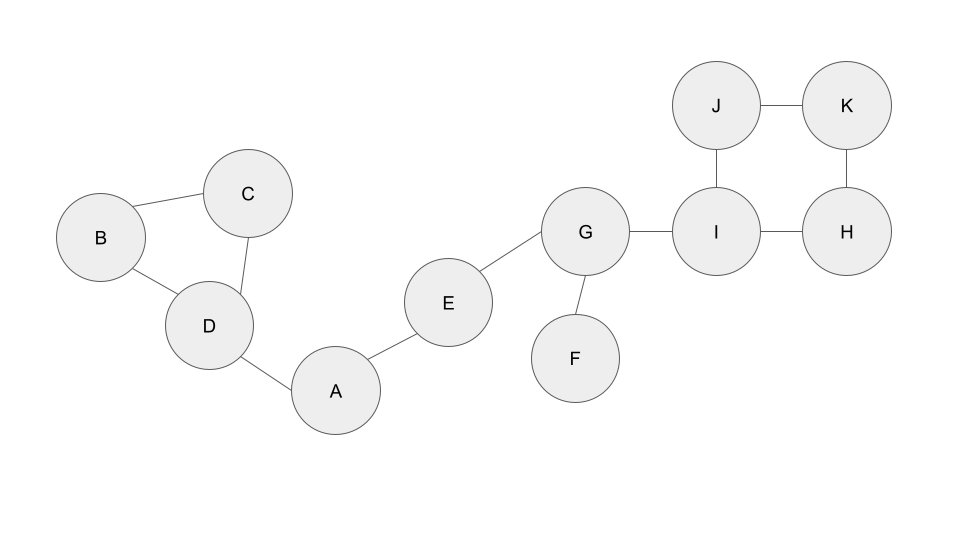
Covering for a Friend (Skiena 7-18)

A Vertex Cover for a graph $G = (V, E)$ is a set $V’ \subset V$ (a subset of $V$ such that ever edge is incident to some $v \in V’$ (formally, $\forall (v_1, v_2) \in E$, either $v_1 \in V’$ or $v_2 \in V’$). Informally, this just means for every edge, at least one vertex on the end of that edge is in $V’$.

Suppose you have $\lvert V \rvert$ people working on $\lvert E \rvert$ projects in teams of 2. You want to organize a meeting where at least one person on each project is present to talk about progress on that project. This is a vertex cover problem — identify the vertices and edges of the implicit graph and convince yourself the solution is a vertex cover!

Skiena 7-18 suggests one algorithm for finding a vertex cover is building a DFS tree and pruning the leaves. Prove, given what you know about edges in a DFS tree, that this is always a vertex cover. Note that by Skiena’s definition, we disallow self-edges in our graphs!

If you’re having trouble, ask for a hint!

Submission

Submit an artifact of your work for one of the two problems.