Activity 17: APSP and Floyd-Warshall

Learning Goals

You will work towards being able to…

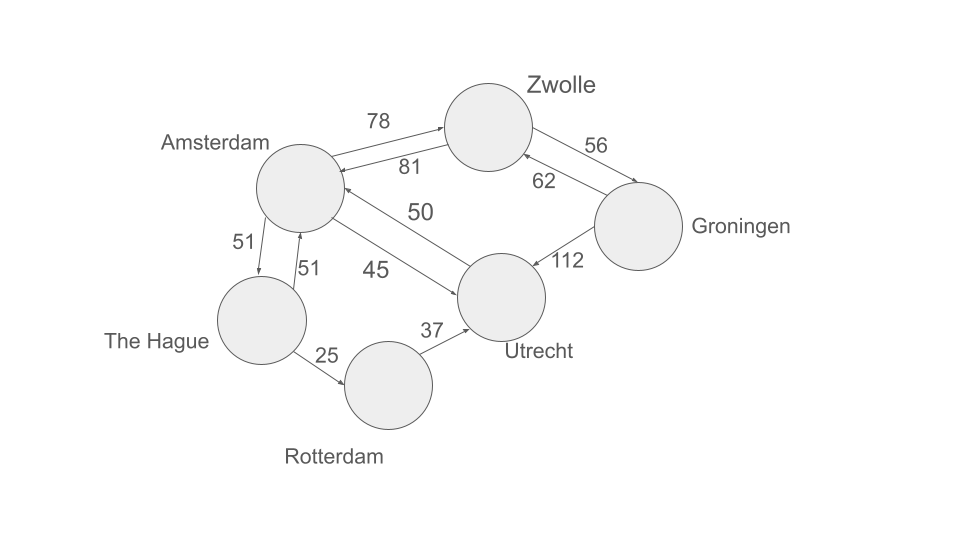
Step through Floyd-Warshall to find the shortest paths between the Dutch cities using the graph below. You should maintain a table that keeps track of the shortest distance between each pair of cities for all of the currently allowed intermediate vertices, updating all of the entries at each iteration.

In the implementation of Floyd-Warshall I showed you, and in the example above, I mentioned that we only need to maintain a single $\lvert V \rvert$ x $\lvert V \rvert$ table of shortest paths so far. However, in the update equation I gave you, $SP(s, t, V’ \cup \{ w \} ) = \min(SP(s, t, V’), SP(s, w, V’) + SP(w, t, V’))$, the elements of the table on the left-hand side of the equation correspond to an updated form of the table and the elements on the right-hand side correspond to an older version of the table (before $w$ was allowed to be an intermediate vertex!). Is this problematic? That is, is it okay that the SPs on the right hand side of the update equation could have possibly had their entries updated already?
Like Dijkstra’s, Floyd-Warshall runs into issues with negative edge weights, but is slightly more robust to them: Floyd-Warshall only fails when there is a negative cost cycle in $G$ w.r.t. $c$. Construct a graph with such a cycle and run Floyd-Warshall. Can you think of a stategy to find negative weight cycles in a graph using Floyd-Warshall?

Hint

What is the cost of the shortest path from $v$ to $v$ for any vertex $v \in V$ if there is a negative weight cycle?

Submit an artifact of your work on Moodle.